Join the Discord →
Learn More →
See Project →
See About page
How to Handle Calculations
Introduction
This page is for the express purpose of helping one with the various ways to deal with calculations. It should be known that on this wiki calculations serve as a supporting measure for a feat and not the main basis. This is due to various reasons:
- The calculations we use are based on rough estimates: A lot of the calculations used are simplified for one to be able to make a calculation within the same day, in real life science calculations are not this easy to make.
- A lot of values are assumed: Due to it being fiction and the author not giving every minute detail of reality, calculations tend to use assumptions and averages in order to get a rough version of where a character stands, thus not being 100% accurate.
- Human error: As with many things, calculations are privy to human error, with the smallest mistake greatly changing a value in calculations.
Due to these reasons listed, calculations can be used to gauge the strength of a feat, but if it goes far beyond what is clearly intended or below what is clearly intended then simply eyeballing the feat is preferred.
Calculators and other utilities
Calculators
Other utilities

Starting Out
Calculations may seem intimidating, but there is a very real and easy way to start getting into them. While being swamped with information may seem overwhelming, taking things piece-by-piece will go miles to easing your newfound endeavor. Though this is a hefty read, it is designed for an individual with almost no mathematical background to learn how to calc from scratch, with most of the resources needed all in one place.
In order to make a calculation, you must first determine what you want to calculate. Once you have a feat in mind, you must begin gaining the necessary information to the calc. Whatever you will need will vary from calc to calc, but keep this in mind: All calculations need to start with at least one value! Finding that value is the first step to completing any calculation. Do not feel like a calculation is impossible due to the amount of variables. After you find one value, it may be much easier to determine the next. I will now go over what needs to be done in order to make a calculation in a very rough outline, from start to finish.
Calc Stacking
Calc stacking refers to the practice of using results from one calculation in order to calculate other feats. Calc stacking is flawed in nature and any calculations that use it will be disregarded almost always. This is due to the level of inconsistency it gives along with inflated results. Through the method any long running franchises could also scale their stats infinitely upwards without actually ever showing any feats in the range they are listed.
Only parameters that can't change between calculations can be repurposed. To provide a few examples:
- Pixel scaling over several steps is permitted, as long as the size of the scaled objects usually stays constant.
- Using the calculated speed of a projectile to calculate the speed of a character dodging said projectile on the very same occasion is usually permitted, as long as the projectile wouldn't have changed its speed mid-flight.
- Using a reliable stated timeframe and reliably stated speed something travels during that time frame one can calculate the distance traveled. Said distance can then usually be used for calculations.
- Multipliers can be used under the conditions lined out on the multiplier page.
- Using speed of characters or attacks calculated at other instances can't be used, as characters and attacks can vary in speed. This is the case regardless of whether the character is seriously trying to do his best or anything similar.
However, even for these parameters calc stacking is avoided as much as possible. That means that results taking less such steps are usually taken over results that rely on more calc stacking.
Calculating Destructive Capacity
In order to determine a character's Destructive Capacity, we must first look through the character's feats, and determine how much energy was exerted to perform such a feat. Sometimes the destructive capacity of the feat can be determined easily with no need of a calculation, but most of the time it isn't as simple. Here we will explain some of the methods we use in order to calculate feats.
Destruction Values
Reference: MPa.m1/2, where m1/2 is 1 (Megapascal per (meter^1))/2. Essentially, we'll divide the MP per meter³ in two which will halve our final result.
Table of Values
Wood

Area under the curve: 16260px 100 kN - 69px 10 mm - 94px
Work of deformation: 16260*(100/69)*(10/94) = 2507J
The specimen is 25x10x15 cm wooden block so its volume is 3750 cm³.
Toughness: 2507/3750 = 0.67 J/cm³
Rocks and Minerals
Limestone

Area under the curve: 166400px 1000 psi - 6.895 MPa - 77px 0.0005 (unitless) - 129px
Limestone's toughness: 166400*(6.895/77)*(0.0005/129) = 0.058 J/cm³.
Sandstone

Area under the curve: 71070px 2000 psi - 13.79 MPa - 79px 0.002 (unitless) - 112px
Sandstone's toughness: 71070*(13.79/79)*(0.002/112) = 0.22 J/cm³.
Igneous Rock
Igneous Rock Stress and Strain
Basalt
The fracture toughness of Icelandic basalt was 2.4 MPa m1/2.
Toughness: 2.4 MPa m1/2 = 1.2 J/cm³
Diamond
Diamond Stress and Strain The Fracture Toughness of diamond is considered "good" to "exceptional", which gets it a value of 3.4 MPa• m½.
Toughness: 3.4 MPa• m½ = 1.7 J/cm³
Ice
Ice toughness value of 145.7 kPa per meter³ (You'll need to download this particular pdf to see the full research).
Ice toughness = 0.1457 J/cm³
Concrete

Area under the curve: 18134px 20 MPa - 77px 0.05% - 56px
Toughness: 18134*(20/77)*(0.05/100/56) = 0.042 J/cm³
Official Source for reference.
Concrete on average has a fracture toughness of 0.2 - 1.4 MPa• m½.
Toughness: 0.2 - 1.4 MPa• m½ = 0.1 - 0.7 J/cm³.
Soil



Area 81492px 0.05MPa - 67px 1% - 84px
Toughness: 81492*(0.05/67)*(0.01/84) = 0.0072 J/cm³
Metallic Elements
Iron
Iron toughness value is on average 135 MPa• m½.
Iron toughness value is 67.5 J/cm³.
Cast Iron
Iron toughness value is on average 81.4 MPa.m1/2.
Cast Iron toughness value is 40.7 J/cm³.
Steel
Maraging Steel (200 Grade) has a fracture toughness of 175 MPa• m½.
Toughness: 175 MPa• m½ = 87.5 J/cm³.
Titanium
Titanium has a fracture toughness of 95.5 MPa• m½.
Toughness: 95.5 MPa• m½ = 47.75 J/cm³.
Nonmetallic Elements
Silicon
Silicon toughness value is 0.8 - 1 MPa.m1/2.
Silicon Toughness = 0.4 J/cm³ - 0.5 J/cm³
TNT Measurements
Most of the time, when calculating Destructive capacity, we end up with extremely large values of energy that are very long to write, also, even if using Orders of magnitude to "shorten" the number, for most people, these large values of energy mean nothing and they cannot rank them easily. That is why we need to convert the numbers we get to TNT measurements, as it is a measuring system that is easier to understand for a wider diversity of people.
To understand the TNT measuring system, we must first explain how it works: 1 gram of TNT contains about 4184 joules of energy. Therefore we can say that every 4184 joules equals 1 gram of TNT, and from here we establish a measuring system:
- 1 gram of TNT = 4184 (j) = 4.184 * 10^3 (j)
- 1 kg of TNT = 1000 gram of TNT = 4184000 (j) = 4.184 * 10^6 (j)
- 1 ton TNT = 1000 kg of TNT = 4184000000 (j) = 4.184 * 10^9 (j)
- 1 kiloton of TNT = 1000 tons of TNT = 4.184 * 10^12 (j)
- 1 Megaton of TNT = 1000 Kilotons of TNT = 4.184 * 10^15 (j)
- 1 Gigaton of TNT = 1000 Megatons of TNT= 4.184 * 10^18 (j)
- 1 Teraton of TNT = 1000 Gigatons of TNT= 4.184 * 10^21 (j)
- 1 Petaton of TNT = 1000 Teratons of TNT= 4.184 * 10^24 (j)
- 1 Exaton of TNT = 1000 Petatons of TNT= 4.184 * 10^27 (j)
- 1 Zetaton of TNT = 1000 Exatons of TNT= 4.184 * 10^30 (j)
- 1 Yottaton of TNT = 1000 Zetatons of TNT= 4.184 * 10^33 (j)
Now, to convert the Energy value to a TNT measurement, we need to divide the energy value by 4.184, and then divide the result of that division by the highest order of magnitude (that is divisible by 3) that is lower/equal to the order of magnitude that was received after the first division, and that will tell you the TNT measurement. For example:
Where does 2*10^24 (j) register on the TNT Measurement system?
(2*10^24) / 4.184 = 4.78*10^23
(4.78*10^23) / 10^21= 478
This was divided by 10^21 because it was the highest order of magnitude that was both divisible by 3 and lower than the order of magnitude of the number that was received after dividing by 4.184, and since the value was divided by 10^21, the TNT measurement is in teratons, according to the chart above:
2 * 10^24 (j) = 478 Teratons.
Mass
When you need to determine the mass of an object, you must first find its volume. Then you must estimate from what type of substance that the object is made out of, as every substance has its own density:
Mass = Volume * Density.
Here is a chart of densities of common materials:
- Continental crust, stone and earth: 2700 Kg/m^3
- Meteors: 3000-3700 Kg/m^3
- Concrete: 2400 Kg/M^3
- Water: 1000 kg/m^3
- Clouds: 1.003 Kg/m^3
Formulas and References
Convertanyunit. Can convert Joules into Ton of Energy equivalents up to Yottatons. Very useful for quick conversion. Doesn't have values for FOE or Ergs.
You can also use Google's online converter.
Basic Formulas Kinetic Energy M * 0.5 * V^2
M = Mass in Kilograms
V = Velocity in m/s
Example:
The fastest car in the world (Hennessey Venom GT) has a top speed of 270 mph, or 120.701 m/s and a weight of 2,743 lbs, or 1244.204 kg
1244.204 * 0.5 * 120.701^2 = 9,063,236.94202 Joules. This is the kinetic energy of the Hennessey Venom GT at top speed.
Potential Energy MGH
M = Mass in Kilograms
G = Gravity in m/s^2 (almost always 9.8)
H = Height as in elevation in meters above ground level.
No real life example, but let's assume that you suspend the aforementioned Hennessey Venom GT in the air by 1 kilometer, or 1000 meters.
1244.204 * 9.8 * 1000 = 12,193,199.2 Joules
Near Total Fatalities
R = Y^(1/3)*0.28
R = Radius in Kilometers
Y = Yield in Kilotons
Let's say you generate an explosion 45.5 kilometers in Radius. Plug that into the equation and solve for Y. I use this calculator to solve for Y.
So plugging the following into that calculator:
45.5 = Y^(1/3)*0.28
According to the calculation, that means Y = 4,291,015.625
Remember, that's the yield in Kilotons
Now to double check, remove the "R =" from the equation and plug the yield into it as such:
4,291,015.625^(1/3)*0.28 = 45.5
Reference Compendium
Conversion Table for Prefixes and Units
Converter for energy values
Gravitational Binding Energy Calculator
Practicing and Tips
You can either try to dive headfirst into original calculations of your own, or you can try to calculate an already accepted calculation from a Calculation Group member without looking at how they did it or the results in order to test your skills! If you choose to do this, try to work through the feat and calculate it. If you choose the same option that the original user did, you can see what their results were. If you got the same or a close result, you know you are on the right track. If your version is wildly different, try to find out what went wrong or what value changed the result.
Practicing can be a vital tool to hone your calcing skills before submitting a formatted blog post to get an original calculation evaluated. There are plenty of calculations out there, so you can practice nearly anything you wish before getting into making official, accepted calculations. Also, if you are having trouble in deciding where to go with a calculation, existing calculations can help you with unusual formulas or applications of anything mentioned here or elsewhere.
Units and Values
This section will give a brief overview of what commonly used values are, and what they mean and are used for.
Distance:
Centimeter: 1/100th of a meter.
Inch: A small imperial measurement. Equal to 2.54 centimeters.
Meter: A standard measurement of distance. Equal to 3.28 feet.
Kilometer: 1000 meters.
Mile: A large imperial measurement. Equal to 1.61 kilometers or 5280 feet.
Light Year: The distance light will travel in one year. Equal to 9.46x10^15 meters, 9.46x10^12 kilometers, or 5.879x10^12 miles.
- Note! Despite the name "light year", this is not a measurement of time. It is purely a measurement of distance. This value is found by taking the speed of light, 299,792,458 meters per second, and multiplying by the number of seconds in a year (31,536,000 seconds).
Energy:
Erg: A very small unit of energy measurement. Equal to 10^-7 joules.
Joule: The SI unit for work or energy.
Watt: Persistent energy measurement. Equal to 1 joule per second, and is equal to a joule in most scenarios.
Ton of TNT: Energy equal to the explosive release of 1 metric ton of TNT. Equal to 4.184x10^9 joules.
FOE: Energy equal to that of a standard supernova. Equal to 10^44 joules.
Formatting an Official Calculation
To make an official, acceptable calculation, make sure to put it in your Blog post. Provide it with a relevant title, feat description, context, and any media used in the calculation (if you use a manga panel, provide the panel; if you pixel scaled a picture or image, profile the edited picture). Explain your work; attempt to make it as easy as possible to read and understand. Preferably, someone who has no experience with calculations should know what you are doing and why you are doing it.
If you feel so inclined you can organize the post further by dividing up the post with two equals signs (==insert section here==) that will divide the post into manageable and quickly comprehensible chunks, and use three apostrophes (insert important text here) to bold important information, such as significant values, formulas, and results.
Once you are done, end the blog post by giving the found values as well as the result in an energy rating/speed as well as our corresponding ratings (e.g. 7.369x10^13 joules, 7-C, Town level). Now upload it to your Blog.
Speed Calculations
Basic Speed Calc
1. For speed, you need two things: Distance and Time. You will need to obtain both of these in order to determine a speed, but focus on one of these two first.
2. In order to determine the time frame, look to the media itself. If the feat is in video format, you can easily determine exactly how long it takes for the feat to be completed. For videos, determining what Frames per second the video runs at and counting the frames can be an extremely accurate way to dictate time. The tool Watchframebyframe can help with this process. Looking at the timestamp from feat start to feet end can be acceptable as well for longer feats. If the media is not video based, see if there is any indication of a time. Does a character speak of how long it took? If so, use this. If not and there is no other way to determine speed, you will need to assume a time frame. If it was a very quick feat, assume 1 second. If it was longer, 1 minute to upwards to 10 minutes can work. Go with whatever makes the most sense in the context of the feat. Once you have this time, convert whatever value you have into seconds.
3. Now that you have a time frame, you need a distance. This can be gathered in a variety of ways. If something within the feat gives you a distance (e.g. Flash stating he just ran around the city), take this and convert whatever distance covered into meters; this conversion to meters applies for pixel scaling and angsizing. Whatever your result is, it must be in meters, The next option is pixel scaling, which will be most commonly used. In order to pixel scale, you will need a program capable of both capturing images and altering them. Two separate programs can be used to achieve this, or a single program if applicable. Gyazo and Paint.net can be used for image capture and alteration, respectively. If you are capturing a YouTube video, try to include the full screen for reference, which is 854x480 pixels when capturing with Gyazo. Once you are able to begin pixel scaling, bring up the full image and begin working. If the distance you want to measure isn't easily found, put it into perspective with another object/character in the shot. You will not always be graced with knowing the distance or height of what you want, so get creative. If there is an adult man in the shot, measure him in pixels and take the average height for men, which is approximately 177 centimeters, and find out how many centimeters/meters each pixel is worth. Once you have this, you can work from there. Sometimes you may need to scale an object to something of known height (X) to an unknown height object (Y) and apply the now found object (Y) height to a new object (Z) that wasn't previously scale-able, due to the lack of a known distance object on screen. Once you have determined how many meters/centimeters a pixel is worth, measure the distance in question to determine the real distance covered. To angsize, follow the guide on our. Remember to convert to meters if you were using any other measurement.
- Note! If the distance is not perfectly angled (not 0, 90, 180, 270, or 360 degrees), you will need to take the height and length, originating for the starting position, and find the hypotenuse to get an accurate distance. Feel free to use Google's hypotenuse calculator or input the formula yourself (c=a^2+b^2, where a^2+b^2 is under the square root symbol). If the distance can be determined by a 90 degree angle, do so to save yourself the time. Paint.net has a built-in angular indicator for the line function.
4. With both distance and time, divide distance covered in meters by time in seconds. S= D/T when S is speed in meters per second, D is distance in meters, and T is time in seconds. This is your result and the calculation is completed!
Speed Calc by Comparison
Oftentimes a distance will not be ascertainable, or it will not be accurate compared to what truly happened. Media often depicts extremely fast characters moving at moderate speeds for the audience's enjoyment; no one wants a fight to end in half a second. In order to determine the speed of such characters, you will need to compare the speed of a known object to that of the unknown. This is primarily done for bullet and lightning dodges.
1. Determine the true speed of the known object. If there is an arrow fired at the character, determine the speed of the arrow. For example, the average speed of a compound bow arrow is about 100 m/s. If you find a speed that isn't in meters per second, convert it to meters per second. If a gun was used, determine what gun it is and the speed of the gun. Google is your friend! Try to use the most scientifically based and accurate source as possible. Remember, if the fact you are looking up isn't common knowledge, you NEED to cite your sources. To put something as a link in source editor, use one bracket containing the link and words; use two for in-wiki articles/sources (e.g. [.[Amon (StarCraft)]] without the period in between the brackets; (https://www.outdoorlife.com/features/chasing-speed-fastest-compound-bow/ 100 m/s) replacing the parenthesis with a single bracket). For lightning this Wiki uses 4.4x10^5 meters per second as the average lightning speed. Once you have your speed, it is time to compare it to the unknown speed object/character.
2. Determine the distance the known object moved. Follow the previous Step 3 of pixel scaling to do this. Once you have the distance for the known object, you need to determine how "fast" it was moving.
3. Find a time frame for the known object. Follow the previous Step 2 in order to do this. Once you have this you can determine the "speed" of your known object.
4. Divide distance over time as done in the previous Step 4. You will now have the speed at which the object appeared to move at, as well as the true speed of the object. Remember, you must get both of these in meters per second. For lightning, take the value of 4.4x10^5 and divide it by the amount you found. This is your multiplier for the unknown character's speed. For example, if the lightning appears to be moving at 63.8349 m/s, you know the scene is moving at 6892.781x faster than normal.
5. Repeat the current Steps 2 to 4 for the unknown object's speed. Once you have that speed you can finish the calc.
6. Multiply your previously determined multiplier by the unknown character's found value to determine the unknown character's true speed. Calculation completed!
There are more advanced ways to find Speed, such as Rotational speed, but most of the less obvious forms of calcing can be learned as you progress.
To calculate the speed of a character or object the basic formula used is v = d/t, where v is the speed of the object, d is the distance the object moved and t is the amount of time it took the character/object to move that much.
Usually the time it took for an object to move the distance is calculated by dividing the distance another object moved during that time, through the speed of that object. That requires knowing the speed of the other object, of course.
More details, such as more in depth explanations on how to figure out the distance and the time as well as examples on how to calculate speed, can be found on the following pages:
Slow Motion Calculations
Sometimes when calculating speed one might encounter scenes where time seems to move slowly from the perspective of a fast moving character. Fundamentally speed calculations can be performed in the same way as normal in such cases.
In other words one just has to figure out a timeframe through the movement of a reference object with known speed, measure how far the character moved during that time frame and divide the distance through the length of the timeframe (v = d/t).
However, sometimes the time is not just slowed down, but appears outright frozen.
In this case, if a reference object with known speed can be visually confirmed to not have moved even 1 pixel (which requires the feat to happen in a visual media like a comic, movie or animation) one can figure out the timeframe, by saying that it must have been less than the timeframe that the object would have taken to move 1 pixel.
If that can not be confirmed, different upper limits, with similar argumentation, can usually be confirmed. In cases with a moving camera/point of view it can be useful to compare the movement to an object that can be assumed to be static.
Especially for written feats another method can be relevant. One first wants to figure out how many times slower the time is from the real time and then figure out how fast a movement in that time really is, based on how fast it looks in the slowed down time.
So the formula would be (real speed of reference object / apparent speed of reference object) * apparent speed of object of interest = real speed of object of interest
For objects moving really slow but aren't frozen, a safe end to use would be 0.1 m/s as 0.1 m/s moves around this fast. Realistically it's faster then standard slow motion movements, but it's a good reference to use as a safe end.
For example: If an object that really is 1000 m/s fast seems to move with only 10 m/s in slowed down time a character that seems to move with a human walking speed of 1.4 m/s in slowed time would move with (1000 m/s / 10 m/s) * 1.4 m/s = 140 m/s.
Useful values for the apparent speed of movement would be:
Sometimes even something like "time seems frozen" or that nothing moves is stated. Often these kinds of statements are hyperboles. However, should that not be the case one may assume that the apparent speed of the reference object is less than or equal to 0.001 m/s.
Mind rule 7 regarding Cinematic Time, whenever calculating feats involving slowed time.
Do not assume that a character viewing the world in slow motion is caused by time dilation. The depiction usually doesn't match the real life phenomena and the effect is commonly caused by the character being able to process events very fast, so that they seem to happen in slow motion to them, instead.
Relativistic to Faster Than Light Speeds
See Requirements for Speed of Light/Faster Than Light Speeds.
Potential Energy
Potential Gravitational Energy: Energy of falling Objects and Energy to lift Objects
Gravitational potential energy is energy an object possesses because of its position in a gravitational field. If an object from a high position falls towards the ground the kinetic energy the object gets from falling is equal to the difference in its gravitational potential energy before and after the fall, provided no other forces such as air resistance act upon it. Vice versa the energy necessary to lift an object to a certain height is also equal to the change in gravitational potential energy of the object before and after being lifted.
However, lifting should generally not be used to calculate Attack Potency unless it is a fast, explosive form of lift (for example: snatch, clean-and-jerk, etc.). This is based on the biomechanics behind how human type characters attack. Unlike a punch, a kick, or most other types of attacks, a lift is a slow sustained motion which allows for many more muscle fibers to be recruited into the movement more easily, generating much more energy than a fast movement used in combat. Lifting movements also allow the body's tendons to help out by storing the energy, then releasing it in a sudden burst, acting like a spring. If we use real world ratios, when the world's heaviest deadlift is compared to the world's most powerful punch, the deadlift has nearly 5 times more energy, demonstrating the disparity between the two types of movements. Similarly, if telekinesis (or any other ability of a similar nature) is used, the lifting must be performed in a timeframe capable of being used as an attack.
In cases close to the ground
In cases where an object is lifted or falls relatively close to the surface of the earth the difference in gravitational potential energy can be calculated using the simple formula
Ep = M*g*h
where
- M = mass of the object in kg
- g = the gravitational acceleration. For earth this is about 9.81 m/s2
- h = how high the object was lifted / how far down the object fell in meter
- Ep = gravitational potential energy difference in joules.
In cases far away from the ground
In cases where an object is lifted very high or falls from very high up the upper formula can not be used any more. Instead the following formula should be used:
Ep = |(G*M*m)/r1 - (G*M*m)/r2|
Where
- G is the gravitational constant, which is 6.674*10−11 N*m2/kg2
- M is the mass of the planet in kg, in case of earth 5.972*1024kg
- m is the mass of the object falling in kg
- r2 is the distance between the center of mass of the planet and the center of mass of the object after the fall / before being lifted (in meters). So usually it is the radius of the planet (in case of earth 6371000 m) + how far the object is away from the ground after the fall / before being lifted.
- r1 is the distance between the center of mass of the planet and the center of mass of the object before the fall / after being lifted (in meters). So usually it is the radius of the planet (in case of earth 6371000 m) + how far the object is away from the ground before the fall / after being lifted.
- Ep is the gravitational potential energy difference in joules.
Terminal velocity
Air resistance is mostly relevant for the case of falling objects and even then can be ignored for most heavy objects like meteors or big constructs.
However for lightweight objects, like for example humans, it becomes relevant.
The air resistance opposes gravity in pulling the object down and due to that slows down the fall of the object, reducing the kinetic energy it gains while dropping.
If an object falls long enough it will reach its terminal velocity and not get any faster than that (provided it wasn't faster to begin with or influenced by other forces than gravity).
Because of that the kinetic energy an object has at terminal velocity often forms a limit to how much energy an object can gain through falling, which means that if our calculated change in potential energy is greater than that we have to consider it as a too high estimate for the energy when reaching the ground.
The terminal velocity of an object can be calculated like described here, but, for example due to the drag coefficient being dependent on the fall speed of the object, it is in practice often difficult to calculate. For a human terminal velocity is approximately 53 m/s close to the ground.
An example of terminal velocity being relevant for the result of a calculation can be found here.
‘’’Note:’’’ Terminal velocity feats should be used mainly for support rather then an absolute as terminal velocity has some forms of biology and can be affected by things such as Impact Resistance.
Attack Potency Calculations
AP can be used to get a variety of stats. For example, AP can lead to finding Durability, Striking Strength, and even uses what you would need to find Lifting Strength, so long as the method you are using needs Mass. With that said, AP is far more variable and can be harder to find than speed. Common forms of AP can usually be seen in Destruction, Explosions, and Kinetic Energy, although there are many more ways to get AP than these (Latent Heat, Gravitational Binding Energy, and more). First you need to determine which method to use before proceeding. Did something get destroyed, cracked, broken, or even vaporized? Use Destruction. If an explosion was set off, use Explosions. If something moves at high speeds, use Kinetic Energy.
- Do note if using Kinetic Energy, do NOT Calc Stack! Calc Stacking occurs when you use a value as determined by another calculation from another scene and use it on your calc (e.g. Using another calc's Speed as a value for your Kinetic Energy).
While this will not be as in-depth as the Speed section, this will briefly overlook what needs to be done in order to find AP results for these three common methods.
Destruction
1. For Destruction, you need to determine volume in cubic centimeters. First, choose the most accurate formula for the object destroyed. See here for geometric formulas.
2. Next, you need to measure the object with either pixel scaling, as shown in the first Step 3, or a statement. Find all the values needed for your formula to be completed. For cubes and spheres, all you will need is a single value. For others you will need more. Remember, if you can't find the object's real size, get creative and look for objects around your target to get a comparison to use. For destruction volume, measure in centimeters.
3. Now that you have the inputs for the formula in centimeters, input in the values in order to get your result in cubic centimeters.
Explosions 1
1. For explosions, all you will need is radius. Get this value in any way you can, and enter the radius into this calculator. Change the megaton yield until your radius value appears. Use the airburst radius (either widespread destruction or near-total fatalities) as your radius.
2. Now take the value you found and divide it by 2. Calculation completed!
Explosions 2
You also have the ability to manually calculate the yield with a formula. This is a bit trickier, but it will help accuracy. If you are interested in using this formula, please view the section below under "Near Total Fatalities". See the explosion radius portion of this page for more information.
Kinetic Energy
1. Kinetic Energy, or KE, is the energy an object holds while moving. The formula is KE = 0.5xMxV^2, where KE is Kinetic Energy in joules, M is mass in kilograms, and V is speed in meters per second. As it would appear, you need to find speed and mass. Find mass. To do this, measure the volume of the object as listed in the Destruction Steps 1 and 2. Sometimes the mass will already be known, such as the mass of a car or human. If this is available to you, use this mass.
2. Now find the density of what is moving. Densities vary by object, so make sure you cite where you have found this density unless it is common knowledge. For example, the density of clouds is 1.003 kg per cubic meter.
- Warning! The value I just gave is in cubic meters. Make sure you use your value appropriately or suffer vastly skewed results.
3. Once you have density and volume, multiply the values to get mass. If everything was done properly, the value you have should now be the mass of the object being moved/moving in kilograms.
4. Obtain speed. See Speed Calcs above for more information on how to obtain speed.
5. Input your obtained speed value in meters per second and your obtained mass value in kilograms. When put into the formula, the result will be your energy in joules. Calculation completed!
Other
There are many other ways to calculate AP, but three notable others are Mass-Energy Conversion, Shearing Force, and Gravitational Binding Energy. The former may only be used if such a method is explicitly stated. If this type of conversion is stated, however, you can use the formula E=Mc^2, where E is energy in joules, M is mass in kilograms, and c is the speed of light in meters per second. Shearing Force is what is used for cutting or slicing feats. Gravitational Binding Energy is the energy needed to bind a planet together, as the name implies, if the planet is destroyed, you will be able to use this formula as a minimum, as its GBE has been overcome. This calculator can find GBE for you, as long as you can provide the values.
Destruction/Creation of Planets and Planetoids
For feats that involve the Destruction or the creation of planets or planetoids, we use a term called Gravitational Binding Energy.
Gravitational Binding Energy
Gravitational binding energy is the energy needed to completely disperse a celestial body. If GBE is broken, the particles of the body will not reform or be bound to each other's gravity, but instead drift off infinitely in the direction they were moved towards. There are precise calculations for this via integration, but a good approximation can be achieved with the following formula:
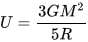
Where U = GBE in joules, M = the mass of the body in question in kilograms, r = its radius in meters, and G = the gravitational constant of 6.67408x10^-11.
For stars, however, the formula is slightly different:
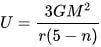
U is GBE in joules, G is the gravitational constant of 6.67408x10^-11, M is mass in kilograms, r is radius in meters, and n is the polytropic value attributed to the type of star. While this formula is not perfectly accurate, it is widely applicable, and is still within the acceptable margin for error.
Ignoring this formula often leads to vast underestimates of the energy required to destroy astronomical objects (for example, some people assume it scales linearly with mass or volume).
Please note that this formula only works on objects that are mostly held together by their own gravity (meaning: large objects in space such as asteroids, moons, planets, stars, etc.) It also doesn't work on black holes, for obvious reasons.
The following is a list of approximate GBE values for various objects:
- Earth's moon (Luna): 1.24e29J
- Earth: 2.487e32J (Calculated with a more accurate method than the above formula)
- OTS 44: 6.906e37J
- VB 10: 3.139e40J
- The sun (Sol): 5.693e41J
- Rigel A: 3.817e42J
SD.net's Planetary Parameter Calculator gives a simplified approach to finding a celestial body's GBE.
Meteors and Kinetic Energy
In order to determine the energy of meteors, we generally use Kinetic energy, as it is the most reliable way to gauge the energy a meteor poses if we are given the required Details.
The equation used:
Ek=0.5*M*V^2
Terms:
Ek=Kinetic Energy
M=mass
V=velocity=speed
There are several speed values that we can use without the need for proof:
If the meteor in question was determined to have come from outer space (or outside of our atmosphere) we will use the value of minimum impact velocity, which is the minimum value of speed an object needs to enter the earth's atmosphere, that value is 11,000 m/s.
If the meteor in question was shown to be Ablated, but didn't come from space, we will use Ablation speeds, which are the minimum speed an object needs to move in order for it to be ablated by its own friction with the atmosphere, the values range from 2000–4000 m/s.
A reasonable high end for meteors that come from outer space is 17,000 m/s, as it is the speed value of most of the meteors that have entered earth's atmosphere.
If the meteor in question wasn't ablated and didn't come from outer space, we will use Potential-Gravitational Energy, as it does not require the use of speed. That is unless we can mathematically find a speed for the meteor.
Creating a real-life hurricane
If a character creates a real-life hurricane, or its winds, the following calculation can be used. What is important is that one is reasonably certain that the hurricane in question covers the same gigantic area as a real one typically does. Usually, characters with the ability to manipulate the weather don't necessarily create one of this size, instead of more local phenomena. Hence a convincing argument regarding the size needs to be made. The following calculation was originally made here by Chris Landsea:
Hurricanes can be thought of, to a first approximation, as a heat engine; obtaining its heat input from the warm, humid air over the tropical ocean, and releasing this heat through the condensation of water vapor into water droplets in deep thunderstorms of the eyewall and rainbands, then giving off a cold exhaust in the upper levels of the troposphere (~12 km/8 mi up).
One can look at the energetics of a hurricane in two ways:
- the total amount of energy released by the condensation of water droplets or ...
- the amount of kinetic energy generated to maintain the strong swirling winds of the hurricane.
It turns out that the vast majority of the heat released in the condensation process is used to cause rising motions in the thunderstorms and only a small portion drives the storm's horizontal winds.
Method 1) - Total energy released through cloud/rain formation: An average hurricane produces 1.5 cm/day (0.6 inches/day) of rain inside a circle of radius 665 km (360 n.mi). (More rain falls in the inner portion of hurricane around the eyewall, less in the outer rainbands.) Converting this to a volume of rain gives 2.1 x 1016 cm3/day. A cubic cm of rain weighs 1 gm. Using the latent heat of condensation, this amount of rain produced gives 5.2 x 10^19 Joules/day or 6.0 x 10^14 Watts.
Method 2) - Total kinetic energy (wind energy) generated: For a mature hurricane, the amount of kinetic energy generated is equal to that being dissipated due to friction. The dissipation rate per unit area is air density times the drag coefficient times the wind speed cubed. One could either integrate a typical wind profile over a range of radii from the hurricane's center to the outer radius encompassing the storm, or assume an average wind speed for the inner core of the hurricane. Doing the latter and using 40 m/s (90 mph) winds on a scale of radius 60 km (40 n.mi), one gets a wind dissipation rate (wind generation rate) of 1.3 x 10^17 Joules/day or 1.5 x 10^12 Watts.
Conclusion:
- Energy to create Hurricane Force winds: 1.5e+12 J / 358.508604207 Tons of TNT, Multi-City Block level
- Energy to create a full Hurricane: 6.01e+14 J / 143.642447418938 Kilotons of TNT, Town level
Explosion Yield Calculations
Step 1: Find the Size of the Explosion
First, you have to find the exact page, or scene where an explosion is shown as a feat. Depending on the environment where the explosion occurred, you may have to scale the size of a smaller object that is shown in the map. Let's do an example...
Example 1: An Explosion Occurs
An explosion of unknown size occurs in this picture, engulfing the object. Find the size of the explosion. The explosion is shown in the below scene.

- The first thing that notice is that you do not know the exact size of the object shown in the picture.
- However, you are allowed to find the size of the object by comparing it with an another object, such as the one shown beside the object.
Step 2: Finding the Radius of the Explosion
From example 1, there is a scene that shows the object in relation to the object shown from the first picture. This is located below. We will use the height of the door as a reference in this case.
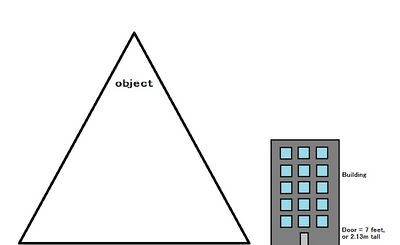
- Given that the door size of the door is 7 feet, or 2.13 meters tall, you can now find the size of the object.
- Log down the size of the object.
- After you have found the size of the object, you compare the size of the object to the diameter of the explosion shown in the first picture.
- Divide the diameter by two to get the radius of the explosion.
Step 3: Finding the Yield of said Explosion
Here is a sample calculator that you can use in order to find the yield of an explosion, provided that you have found the exact diameter of it. Keep note that if the explosion is against a surface it is preferred, but not required, that you use the surface detonation setting on this calculator.
- Generally, you take the near-total fatalities section from the list of calculated values/calculator above.
- As for why it is used, the definition of near-total fatalities states that: all large above-ground structures are destroyed within that radius, as well as causing 100% fatalities to anyone that is affected within the radius due to sheer pressure alone.
- When you get the result of said explosion, you multiply the value by 0.5. This is because only 40 to 50 percent of the total energy of the explosion is actually from the blast.
- Keep in mind that if the explosion is an actual nuclear explosion, you can disregard the point above.
If you are having a hard time using the nuclear calculator, this equation can be used to find the yield of said explosion.
- Air blast radius (near-total fatalities) Yield: Y = ((x/0.28)^3)/1000 with Y in megatons of TNT and x the radius in km.
However, the rules above are for explosions happening in mid-air. For explosions that happen on the ground, we use this formula:
- W = R^3*((27136*P+8649)^(1/2)/13568-93/13568)^2, where W is the yield in tons of TNT, R is the radius in meters, and P is the shockwave pressure in bars, where we generally use 1.37895 bars or 20 psi of pressure.
Durability From Tanking an explosion
Let's say an explosion occurs and a character endures the explosion. If that explosion doesn't occur close to the character the amount of energy that hits it will be significantly lower than the full energy of the explosion. To find the actual amount of the energy from the explosion that he/she tanks one first applies the inverse square law.

What does the inverse square law state?
- The further you are away from an explosion, the less damage you will take from it. That is, because the power of said explosion is distributed over a larger and larger surface area as the distance from the epicenter increases.
- The surface area of a sphere is A = 4πr^2. This is relevant because when an explosion occurs, the energy of said explosion radiates outwards as a sphere, unless obstructed. If it happens on the ground the explosion is restricted in the downwards direction and hence only expands in half a sphere, meaning A = (4πr^2)/2. Other surface areas are imaginable as well.
- The intensity of said explosion at a distance of r is I = P/A, where I = Joules of energy, A is as above and P=Power/Yield of explosion, in Tons of TNT.
- I is a measure of Energy per Area (J/m^2 in SI units).
How does that relate to the durability needed to survive an explosion?
- The amount of energy that hits a target if r meters away from an explosion is E=I*CA, where I is calculated as described above and E is the energy the target is hit by. CA is the crossectional area of the target. That is the area of the largest cross section of the target that is orthogonal to the direction the explosion expands into. That is not half the surface area of the target, but less than that. For a sphere for instance this would not be 4*pi*r^2 / 2, but instead pi*r^2 as that is the area of the largest cross-section which, in this case, is a circle with the same radius as the sphere laid through its center (in such a way that it is orthogonal to the expansion of the explosion).
- It should be noted that the above idea of calculating it via the cross sectional area is strictly speaking a simplification that works well when the size of the target is small when compared to that of the explosion at the point it hits it. If one imagines the source of the explosion as a lightsource and the shockwave of radius r as a sphere or dome, then the area of the shadow that the object throws on the sphere/dome is the precise area to be used. This is, in general, considerably more difficult to calculate, though. The cross sectional area as explained above will generally provide an underestimation of the area in question.
- CA is approximately 0.68 m^2 for a grown human. It can also be estimated as half of the body's surface area calculated using this, but that is a slight overestimation.
Let's do an example.
Example
An omnidirectional explosion of 7 kilotons of TNT occurs, and a human 30 meters away from the epicenter endures the explosion. How high is the durability of the human?
- First, we set P = 7000 Tons of TNT, as that is the yield of said explosion.
- Second, we set the radius, or r = 30m
- Third, we find the value of I, or the intensity of the explosion at a specific distance.
- I = (7000 Tons of TNT) / (4π((30m)^2))
- This means at 30 meters away from the epicenter of the explosion, the shockwave is hitting with an intensity of I = 0.619 Tons of TNT per m^2.
- CA = 0.68 m^2 for a human.
- So I*CA = 0.619 Tons of TNT per m^2 * 0.68 m^2 = 0.42092 Tons of TNT = E.
- The character can withstand a 0.42092 Tons of TNT blast, meaning Building level durability.
Explosion Radius
The aim of this page is to find the area (near-total fatalities) that an explosion should cover to reach a certain AP tier.
Using the formula from, R = Y^(1/3)*0.28, where Y is the yield in kilotons and R the radius in km, so that:
- Yield*2 ==> Radius*2^(1/3) = Radius*1.26
- Yield*5 ==> Radius*5^(1/3) = Radius*1.71
- Yield*10 ==> Radius*10^(1/3) = Radius*2.1544
Since the calculator didn't give results below 1 kiloton, the above would be useful; using these lists we will find the required area.
Nuclear Explosions
These values can only be used when the detonation has a nuclear origin.
- Room level (4.8 - 17.7 m) = The size of a Tennis court, the size of a Volleyball court, the area of a typical three-bedroom house
- Building level (17.7 - 35.3 m) = The surface of a Olympic-size swimming pool
- Large Building level (35.3 - 62.3 m) = An American football field area, a Soccer field area, a Baseball field area (including outfield), Hagia Sophia
- City Block level (62.3 – 130 m) = A cricket field area, a common city block from Manhattan, the Pyramid of the Sun area
- Multi City Block level (130 – 280 m) = Great Pyramid of Giza area (min)
- Multi-City Block level (280 – 500 m) = The Vatican City, The Pentagon
- Town level (0.5 - 1.3 km) = The City of London
- Town level (1.3 - 2.7 km) = The Smallest Oceania islands (min), Machu Picchu
- City level (2.7 – 5 km) = Nauru (min), Manhattan Island
- City level ( 5 - 12.5 km) = Teotihucan (min), Taipei City, Disney World, Paris (inner city), Washington D.C., Hollywood, Brooklyn
- Metropolis level (12.5 – 28 km) = wikipedia:es:Andorra:Andorra (min), Los Angeles, Hong Kong, Tokyo
- Metropolis level (28 - 45.5 km) = Luxembourg (min), Trinidad Island
- Island level (45.5 – 130 km) = Jamaica, Belgium, Puerto Rico, Israel, Netherland, Yellowstone National Park
- Large Island level (130 – 280 km) = Austria, South Korea, North Korea, Greece, Great Britain, Cuba, Benelux
- Country level (280 - 535.6 km) = Philippines, Japan, Spain, Turkey, Germany, France
- Country level (535.6 – 1300 km) = Egypt, Alaska State, Mexico, Greenland, Argentina, India
- Country level (1300 – 2555 km) = Australia, Brazil, China, United States of America, Antarctica, the area of Pluto, Russia, Canada, South America, Europe
- Continent level (2555 – 4600 km) = Africa, the area of the Moon, The Americas, Asia
- Multi-Continent level (4600 - 86614.1 km) = The Area of Mars, the area of Earth, the area of Neptune
Large Size Calculations
In fiction, there are many characters of Large Size. When it comes to tiering them their size alone can be an indicator of their statistics. This page explains which statistics can and can't be calculated from size alone.
Attack Potency
The physical attack potency, and with it the durability, can be estimated from the size of a character alone.
That follows a simple conservative estimation: Any character can at least just fall into someone. In other words, their potential energy can be used to attack. The only prerequisite to this method is that the character should be at least Type 0 Size on the Large Size scale.
In order to perform the calculation one will need the mass of the character and its center of mass.
The center of mass of a human-shaped character is about 10 cm below the navel, albeit this varies from individual to individual. Generally one can estimate that it is around 50% of the body height up.
In order to find the mass of the character, upscaling methods are helpful. If the character is x-times larger than its normal-sized counterpart, and made of roughly the same materials, then its mass would be about x^3-times larger.
With this information, the energy can be calculated via the usual GPE methods.
Except for very large characters that is simply "Potential energy = mass*9.81*height of center of gravity". Mass should be in kilogram and height in meter. The result is in joule.
An alternative method to calculate Attack Potency from size is from Kinetic Energy. There one takes the mass of the character and uses its running speed to get Kinetic Energy via "Kinetic Energy = 0.5*Mass*(Running speed)^2". Here mass should be in kilograms and running speed in meters per second. The result is in joule.
The best practice is to measure the speed directly from the source material. Should that not be possible, but it is known that the character moves relative to its size as fast or faster than its normal-sized counterpart, upscaled speed can be used. To confirm that they are that fast, it must be clear that they, for instance, take steps within the same timeframe or less than a normal human would. If that is the case, then their speed should be x-times higher than that of their normal-sized counterpart, if they are x-times larger.
Lifting Strength
Lifting Strength should not be calculated from size. While characters have to lift more body weight, lifting strength is the weight they can lift in addition to that. There is no way of telling how much more that is.
Speed
As mentioned in the AP section, speed can under circumstances be taken from size. An x-times larger character should also be x-times faster. However, strict confirmation is necessary.
Standard Tables
Average Female Height = 1.595m
Average Sprinting Speed = 5.55 m/s (approx. based on this and this)
We will assume that the density of the giant is equal to that of an average human.
The table is based on the gravitational potential energy and uses the method regarding that explained in the Attack Potency section above.
Earthquake Feats
Overview
An earthquake (also known as a quake, tremor or temblor) is the perceptible shaking of the surface of the Earth. Earthquakes can be violent enough to toss people around and destroy whole cities. Such earthquakes being caused by characters are a method useable to determine Attack Potency.
For the purpose of these calculations shaking a minor area should not be assumed to automatically translate to an earthquake. Either a large area being shaken or evidence that we are dealing with something earthquake-like and not just some minor shaking would be needed.
One has to differentiate between different ways an earthquake was caused, if one wants to calculate the energy.
Case 1: Meteor impact
This is the easiest method to determine the necessary energy to cause an earthquake, even though not the most commonly used one.
In which cases should it be used?
This method should be used if an earthquake is caused through the impact of a meteor or through an event very similar to that.
How is it done?
Step 1:
First step is to determine the distance of a place, for which we know which effects the earthquake had on, to the epicenter. To clarify: The epicenter is the point on the Earth's surface that is directly above the hypocenter or focus, the point where an earthquake or underground explosion originates. From the rest this calculator will be used.
Step 2:
Input the distance from the epicenter, which was determined in Step 1, in the "Distance from Impact" field.
After that input the rest of the values, for now it doesn't matter what stands in the rest of the fields.
Press "calculate effects".
If the inputs were sufficiently high on the page that appears will be a section named "Seismic effects".
In that section descriptions are given which describe the effects of an earthquake, which was caused by a meteor with the properties described by the prior input. Specifically this are the effects at the input distance from the epicenter.
All possible descriptions are listed in Table 1. What one now wants to do is to change the input values, except the "Distance from Impact" value, so long until you have the lowest values, for which still the description best fitting for the effects at your chosen distance from the epicenter is shown.
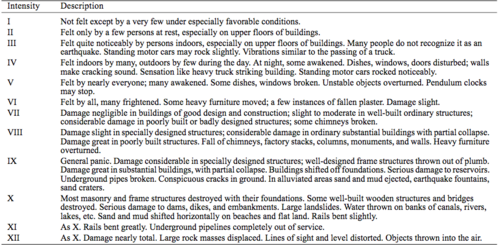
Step 3:
If you have found these values take a look at the "Energy" section above the "Seismic Effects" section on the page. The value given for "Energy before atmospheric entry" is the energy of your (theoretical) meteor and with that also the energy necessary to cause the earthquake.
Case 2: Natural Earthquakes
This method doesn't find much use, but is worth mentioning.
In which cases should it be used?
This method should only be used in case a natural earthquake occurs, as it takes into account the work necessary to overcome the friction between continent plates etc.
It should be noted that, realistically speaking, a natural earthquake can't have a magnitude above about 9.6. So if the richter scale magnitude calculated is above that, this methodology should only be used if special circumstances apply.
How is it done?
First perform step 1 and step 2 like described in "Case 1: Meteor Impacts".
Since here one does not wish to know the energy necessary for a meteor, but for a real earthquake this time the third step has to be different.
Instead of looking at the "Energy" section, one looks at the "Seismic Effects" section again. There a value named "Richter Scale Magnitude" will be listed. This is the magnitude an earthquake would need to have to cause the described effects at the distance from the epicenter we input. The value is independent from the method through which the earthquake was caused, so it also stays true for other natural earthquakes which aren't caused by meteor impacts.
One takes the Richter Scale Magnitude and inputs it in this calculator in the "Earthquake Magnitude" field. Then press the compute button.
The value for "Total "Seismic Moment Energy" (MO)" is the energy necessary to cause such an earthquake.
Case 3: Other
This is the most common method to calculate earthquakes.
In which cases should it be used?
This should be used if the earthquake is not caused by something very similar to a meteor impact and is also not a natural earthquake.
How is it done?
The method is identical to that of "Case 2: Natural Earthquakes", just this time instead of the "Total Seismic Moment Energy" (MO)" value our end result is the "Seismic Energy in Waves Radiated from Earthquake Source" value.
The reason one uses that value in this case is that the big energy loss that comes through the movement of the continental plate or similar processes of natural earthquakes is not present here. Instead we can only use the amount of energy that actually takes part in the effects we observe. Hence only the energy radiated in the form of seismic waves is relevant for this case.
Alternative Method to determine Richter Magnitude
A more direct method to figuring out the result is the following.
1. Mercalli Intensity to Magnitude at distance
The first step is the figure out the (Richter) Magnitude the earthquake corresponds to at the distance from the epicenter (origin) it is felt at. To do that we look at Table 1 above and pick the appropriate Intensity. Then we use that intensity to pick the appropriate "Magnitude at distance" from the table below.
| Magnitude at distance | Mercalli Intensity |
|---|---|
| 1-2 | I |
| 2-3 | I-II |
| 3-4 | III-IV |
| 4-5 | IV-V |
| 5-6 | VI-VII |
| 6-7 | VII-VIII |
| 7-8 | IX-X |
| 8-9 | X-XI |
| 9+ | XII |
2. Magnitude at distance to Magnitude at origin
To do this knowing how far away from the origin we measured the Magnitude at distance is necessary. We call that distance r (unit should be km). To figure out how much the actual magnitude of the earthquake is we differentiate between 3 cases.
- r < 60km: In this case the formula is (Magnitude at distance) + 0.0238*r = Richter Magnitude of Earthquake
- 60 ≤ r < 700 km: In this case the formula is (Magnitude at distance) + 1.1644 + 0.0048*r = Richter Magnitude of Earthquake
- r ≥ 700 km: In this case the formula is (Magnitude at distance) + 6.399 + 1.66*log10((r/110)*((2*π)/360)) = Richter Magnitude of Earthquake
3. Richter Magnitude to Energy
To get the energy from the Richter Magnitude we differentiate between 3 cases on how the earthquake was created:
- Meteor Impact: The formula is 10(Richter Magnitude + 5.87)/0.67 = Energy in Joules
- Real Earthquake: Just use this calculator. The Total Seismic Moment Energy is the result.
- Others: Used for any artificially created earthquakes or earthquakes that aren't the former two. The formula is 101.5*(Richter Magnitude)+4.8 = Energy in Joules
Earthquake Chart
Overview
This is a basic chart that yields the output of Earthquakes from Magnitude 1 to 10.5
You can use this and this chart to estimate the appropriate magnitude.
Radiated Waves
| Magnitude | Joules | Tons | Tier |
|---|---|---|---|
| Magnitude 1 | 1.995262e+6 | 0.000476879063098 Tons | Wall level |
| Magnitude 1.5 | 1.122018e+7 | 0.0026816873805 Tons | Wall level |
| Magnitude 2 | 6.309573e+7 | 0.0150802413958 Tons | Wall level |
| Magnitude 2.5 | 3.548134e+8 | 0.0848024378585 Tons | Room level |
| Magnitude 3 | 1.995262e+9 | 0.476879063098 Tons | Small Building level |
| Magnitude 3.5 | 1.122018e+10 | 2.6816873805 Tons | Small Building level |
| Magnitude 4 | 6.309573e+10 | 15.0802413958 Tons | City Block level |
| Magnitude 4.5 | 3.548134e+11 | 84.8024378585 Tons | City Block level |
| Magnitude 5 | 1.995262e+12 | 476.879063098 Tons | City District level |
| Magnitude 5.5 | 1.122018e+13 | 2.6816873805 Kilotons | Town level |
| Magnitude 6 | 6.309573e+13 | 15.0802413958 Kilotons | Town level |
| Magnitude 6.5 | 3.548134e+14 | 84.8024378585 Kilotons | Town level |
| Magnitude 7 | 1.995262e+15 | 476.879063098 Kilotons | Town level |
| Magnitude 7.5 | 1.122018e+16 | 2.6816873805 Megatons | City level |
| Magnitude 8 | 6.309573e+16 | 15.0802413958 Megatons | City level |
| Magnitude 8.5 | 3.548134e+17 | 84.8024378585 Megatons | City level |
| Magnitude 9 | 1.995262e+18 | 476.879063098 Megatons | Metropolis level |
| Magnitude 9.5 | 1.122018e+19 | 2.6816873805 Gigatons | Island level |
| Magnitude 10 | 6.309573e+19 | 15.0802413958 Gigatons | Island level |
| Magnitude 10.5 | 3.548134e+20 | 84.8024378585 Gigatons | Island level |
Total Seismic Energy
| Magnitude | Joules | Tons | Tier |
|---|---|---|---|
| Magnitude 1 | 3.899420e+10 | 9.3198374761 Tons | Large Building level |
| Magnitude 1.5 | 2.192805e+11 | 52.4092973231 Tons | City Block level |
| Magnitude 2 | 1.233105e+12 | 294.71916826 Tons | City District level |
| Magnitude 2.5 | 6.934258e+12 | 1.65732743786 Kilotons | Town level |
| Magnitude 3 | 3.899420e+13 | 9.3198374761 Kilotons | Town level |
| Magnitude 3.5 | 2.192805e+14 | 52.4092973231 Kilotons | Town level |
| Magnitude 4 | 1.233105e+15 | 294.71916826 Kilotons | Town level |
| Magnitude 4.5 | 6.934258e+15 | 1.65732743786 Megatons | City level |
| Magnitude 5 | 3.899420e+16 | 9.3198374761 Megatons | City level |
| Magnitude 5.5 | 2.192805e+17 | 52.4092973231 Megatons | City level |
| Magnitude 6 | 1.233105e+18 | 294.71916826 Megatons | Metropolis level |
| Magnitude 6.5 | 6.934258e+18 | 1.65732743786 Gigatons | Island level |
| Magnitude 7 | 3.899420e+19 | 9.3198374761 Gigatons | Island level |
| Magnitude 7.5 | 2.192805e+20 | 52.4092973231 gigatons | Island level |
| Magnitude 8 | 1.233105e+21 | 294.71916826 Gigatons | Island level |
| Magnitude 8.5 | 6.934258e+21 | 1.65732743786 Teratons | Country level |
| Magnitude 9 | 3.899420e+22 | 9.3198374761 Teratons | Country level |
| Magnitude 9.5 | 2.192805e+23 | 52.4092973231 Teratons | Country level |
| Magnitude 10 | 1.233105e+24 | 294.71916826 Teratons | Country level |
| Magnitude 10.5 | 6.934258e+24 | 1.65732743786 Petatons | Continent level |
Volcanic Eruptions
Overview
The aim of this page is to find the values of Volcanic Eruptions from the official Volcanic Explosivity Index (VEI) scale. Do note the energy of a volcanic eruption can vary widely thus these are just rough estimates.
Volcanic Eruptions Chart
| VEI Level | Eruption Type | Joules | Tons | Tier | Description |
|---|---|---|---|---|---|
| VEI 0 | Effusive (Non-Explosive) | ~1.0e+10 J | ~2.4 Tons | Small Building level | Gentle lava flow without significant explosions, common in shield volcanoes like Kilauea. |
| VEI 1 | Small Hawaiian/Strombolian | ~1.0e+12 J | ~240 Tons | City Block level | Small explosive bursts of gas and lava, like Stromboli’s regular eruptions. |
| VEI 2 | Moderate Strombolian/Vulcanian | ~1.0e+14 J | ~24 Kilotons | Town level | Short-lived explosions, producing ash columns up to 5 km high, seen in volcanoes like Etna. |
| VEI 3 | Large Vulcanian/Sub-Plinian | ~1.0e+15 J | ~240 Kilotons | Town level | Significant ash clouds (10-15 km high) with pyroclastic flows, similar to the 1991 Mount Unzen eruption. |
| VEI 4 | Sub-Plinian | ~1.0e+17 J | ~24 Megatons | City level | Ash plumes reaching 20 km, widespread tephra deposits, as seen in the 2010 Eyjafjallajökull eruption. |
| VEI 5 | Plinian (e.g., Mount St. Helens) | ~1.0e+18 J | ~240 Megatons | Metropolis level | Highly explosive eruption with a column over 25 km, massive pyroclastic flows, and widespread devastation. |
| VEI 6 | Large Plinian (e.g., Krakatoa 1883) | ~1.0e+19 J | ~2.4 Gigatons | Island level | Can destroy entire islands, create tsunamis, and alter global climate. The 1883 Krakatoa eruption was heard 3,000 miles away. Volcanoes at this level, such as Krakatoa, have unleashed around 200 megatons of TNT. |
| VEI 7 | Supervolcanic (e.g., Tambora 1815) | ~1.0e+21 J | ~240 Gigatons | Island level | Capable of covering continents in ash and drastically lowering global temperatures. Tambora caused the "Year Without a Summer." |
| VEI 8 | Supervolcanic (e.g., Yellowstone scale) | ~1.0e+23 J | ~24 Teratons | Country level | Rare catastrophic event that could cause mass extinctions, blanketing the Earth in ash and disrupting ecosystems for decades. |
Cloud Calculations
Due to being virtually always present, clouds are one of the most common objects affected by the attacks or powers of characters. As such, how to calculate feats involving the creation, destruction or movement of clouds is of common interest.
Cloud Volume
The first step necessary for any cloud calculation is determining how much of a certain cloud was affected (created, destroyed or moved). Pixel scaling is the most reliable way to do so and the first thing one should try to do. However, in case of clouds there often is nothing one could scale from. Hence other practices are often relevant.
Characteristic Cloud Thickness
Different types of clouds have a characteristic thickness to them. The thickness is the distance from the lower border to the upper border of the clouds. If clouds can't be directly scaled this is usually the only way to figure out the height to use for the calculation of the affected cloud volume.
| Cloud Type | Description | Characteristic Thickness | Appearance |
|---|---|---|---|
| cirrus | Generally characterized by thin, wispy strands. They are usually white or light gray in color. Since cirrus clouds arrive in advance of the frontal system or tropical cyclone, it indicates that weather conditions may soon deteriorate. While it indicates the arrival of rain, cirrus clouds only produce fall streaks (falling ice crystals that evaporate before landing on the ground). | 100m to 8000m, with 1500m on average.[1] |  |
| stratus | Low-level clouds characterized by horizontal layering with a uniform base. They vary from dark gray to nearly white. Stratus clouds may produce a light drizzle or a small amount of snow. These clouds are essentially above-ground fog formed either through the lifting of morning fog or through cold air moving at low altitudes over a region. | Less than 1000 meters[2][3] |  |
| cumulus | Clouds which have flat bases and are often described as "puffy", "cotton-like" or "fluffy" in appearance. Cumulus clouds are often precursors of other types of clouds, such as cumulonimbus. Normally, cumulus clouds produce little or no precipitation. | 600m to 2000m[4][5] |  |
| stratocumulus | Clouds characterized by large dark, rounded masses, usually in groups, lines, or waves. They look much like cumulus clouds, except lumped together and bigger. | Less than 1000 meters,[6][7] of the order of 100m[8] |  |
| Nimbostratus | A cloud with a diffuse cloud base. Although usually dark at its base, it often appears illuminated from within to a surface observer. Typical rain clouds. | 2000m to 4000m[9] |  |
| cumulonimbus | Dense, towering vertical clouds. They are the clouds that usually accompany heavy rain, storms and thunderstorms. | Usually between 8000m to 11800m.[10] Sometimes as few as 2000m in polar air.[11] |  |
Volume
Using the two values from above one can approximate the volume of the clouds. Formula model the clouds as the intersection of a spherical shell and a spherical sector. However, usage of those usually isn't necessary with the normal distances.
Cloud Mass
In order to determine the cloud mass from its volume one simply has to multiply it with the clouds density. However, what a clouds density is can be defined in two different ways
- The density of the water in the cloud.
- The density of the water and air in the cloud together.
Which to use depends on which way the cloud was affected. Chemical changes, like vaporization or condensation of water use the first density, while movement changes like the creation of instabilities or changing the clouds position or shape use the second density.
The density of the water and air in the cloud together is approximately 1.003 kg/m3.
The density of just the water in the cloud is the liquid water content. The liquid water content depends on the cloud type. Following values can be used as orientation:
| Cloud Type | Liquid Water Content (g/m3) |
|---|---|
| cirrus | 0.03 |
| fog | 0.05 |
| stratus | 0.25 to 0.3 |
| cumulus | 0.25 to 0.3 |
| stratocumulus | 0.45 |
| Nimbostratus | nearly 1[12] |
| cumulonimbus | 1 to 3 |
Lightning Calculations
Lightning calculations are normally used for when a character creates or summons an incredibly large lightning bolt. There can be other situations for when this is used, but the most simplistic cases in fiction are for this.
The calculation process for this is broken down into 3 formulas:
Potential Difference (V) Calculation
V = E x d
- V is the potential difference (voltage)
- E is the electric field strength
- d is the distance (meters)
Capacitance (C) Estimation
C ≈ ϵ0 × (A/d)
- C is the capacitance
- ϵ 0 is the permittivity of free space (8.854×10^−12 F/m)
- A is area
- d is distance (meters)
Energy (W) Calculation
W=1/2CV^2
- W is the energy stored
- C is the capacitance
- V is the potential difference
Notes and Sources
- Source: Alabamaquake
- Total Seismic Energy should only be used for real earthquakes. It shouldn't be used for physical earthquakes or earthquakes caused through abilities.
- Shaking a minor area should not be assumed to automatically translate to an earthquake. Either a large area being shaken or evidence that we are dealing with something earthquake-like and not just some minor shaking would be needed.
- The energy required to shake the Earth.
- ↑ wikipedia:Cirrus cloud
- ↑ https://www.sciencedirect.com/topics/earth-and-planetary-sciences/stratus-clouds
- ↑ http://www.ias.sdsmt.edu/dept/clouds-intro.htm
- ↑ http://www.ias.sdsmt.edu/dept/clouds-intro.htm
- ↑ wikipedia:de:Cumulus
- ↑ https://www.sciencedirect.com/topics/earth-and-planetary-sciences/stratus-clouds
- ↑ http://www.ias.sdsmt.edu/dept/clouds-intro.htm
- ↑ https://journals.ametsoc.org/doi/pdf/10.1175/1520-0469%281950%29007%3C0054%3AVALWCI%3E2.0.CO%3B2
- ↑ wikipedia:Nimbostratus cloud
- ↑ wikipedia:Cumulonimbus cloud
- ↑ http://www.ias.sdsmt.edu/dept/clouds-intro.htm
- ↑ http://pernerscontacts.upce.cz/24_2011/Krollova.pdf